Understand Stack and Their Implementation Using Array [06]

Introduction

A stack is a fundamental data structure in computer science, essential for managing and organizing data in a specific order. The stack follows a Last In, First Out (LIFO) principle, meaning that the last element added to the stack is the first one to be removed. This behavior is similar to a stack of plates, where the last plate placed on top is the first one to be taken off.

Key Characteristics of a Stack:

LIFO (Last In, First Out): The last element added is always the first one to be removed.
Push and Pop Operations: Elements are added to (push) or removed from (pop) the top of the stack.
Limited Access: Only the top element is accessible for viewing or modification, not the other elements beneath it.

Visualizing a Stack:

Imagine a stack of books. When you add a new book, it goes on top of the stack. If you want to remove a book, you have to take the top one. The same rule applies in programming with stacks.

Applications of Stacks:

Stacks are used in a variety of computer science problems. Here are a few examples:

Undo/Redo Functionality: Stacks are used to keep track of changes in applications, enabling users to undo or redo actions.
Expression Evaluation: In mathematics and programming, stacks are used to evaluate expressions like postfix or infix.
Function Call Management: When functions are called, the system pushes them onto the call stack, and once the function finishes, it is popped off.

Stack Operations

Stacks support a few essential operations that allow efficient management of the data. These operations are designed to work according to the LIFO (Last In, First Out) principle.

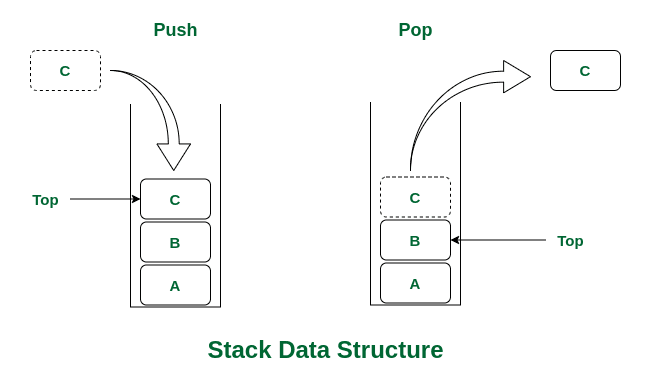
Push: Adding an Element to the Stack

The Push operation adds an element to the top of the stack. If there’s space in the stack (in case of a fixed-size stack), the new element is inserted on top of the current top element.

Pseudocode:

Push(stack, element):
    if stack is not full:
        increment top index
        stack[top] = element
    else:
        print "Stack Overflow"

Pop: Removing the Top Element

The Pop operation removes the top element from the stack and returns it. After removal, the top pointer is decremented to point to the next element in the stack.

Pseudocode:

Pop(stack):
    if stack is not empty:
        element = stack[top]
        decrement top index
        return element
    else:
        print "Stack Underflow"

Peek/Top: Viewing the Top Element

The Peek or Top operation allows you to view the top element of the stack without removing it. This is useful when you want to see what the current top element is but do not want to modify the stack.

Pseudocode:

Peek(stack):
    if stack is not empty:
        return stack[top]
    else:
        print "Stack is Empty"

isEmpty: Checking if the Stack is Empty

The isEmpty operation checks whether the stack is empty. If the top index is -1 (or an equivalent value depending on the implementation), the stack is considered empty.

Pseudocode:

isEmpty(stack):
    if top == -1:
        return true
    else:
        return false

isFull: Checking if the Stack is Full

The isFull operation checks if the stack has reached its maximum capacity. This is particularly relevant in stack implementations using arrays, where a fixed-size array is used to hold elements.

Pseudocode:

isFull(stack):
    if top == maxSize - 1:
        return true
    else:
        return false

These operations form the core functionality of a stack and are crucial for its proper management and utilization in various algorithms and data structures.

Advantages and Limitations of Stacks

Advantages:

Simple Data Management: Efficient LIFO structure, with fast operations like push, pop, and peek.
Memory Efficiency: Low overhead, using memory proportional to the number of elements.
Versatile Use Cases: Essential in function call management, undo/redo, expression parsing, and data reversal.
Easy to Implement: Simple to implement with arrays or linked lists, with O(1) time complexity for main operations.

Limitations:

Fixed Size (Array Implementation): Limited capacity, leading to stack overflow if full.
Limited Element Access: Can only access the top element, requiring pops to access deeper elements.
Memory Wastage: Fixed-size stacks may waste memory if not fully utilized.
Limited to LIFO: Not ideal for tasks requiring other access patterns (e.g., FIFO).

Implementing a Stack Using Arrays

Here’s a full implementation of a stack using arrays in C++.

Define the Stack Class

We start by defining the stack class and initializing it with a maximum size of 3 for the stack.

#include <iostream>
using namespace std;
 
#define MAX_SIZE 3  // Limiting the stack size to 3 for simplicity
 
class Stack {
private:
    int stack[MAX_SIZE];  // Array to store stack elements
    int top;              // Index of the top element
 
public:
    // Constructor to initialize the stack
    Stack() {
        top = -1;  // Initialize the top index to -1 (indicating the stack is empty)
    }
};

Code for the Push Operation

Next, we define the push function that adds an element to the stack. If the stack is full, it prints a "Stack Overflow" message.

// Push operation: Adds an element to the stack
void push(int element) {
    if (top < MAX_SIZE - 1) {
        top++;
        stack[top] = element;
        cout << "Pushed " << element << " to stack." << endl;
    } else {
        cout << "Stack Overflow" << endl;
    }
}

Code for the Pop Operation

The pop function removes the top element from the stack. If the stack is empty, it prints a "Stack Underflow" message.

// Pop operation: Removes the top element from the stack
int pop() {
    if (top != -1) {
        int element = stack[top];
        top--;
        return element;
    } else {
        cout << "Stack Underflow" << endl;
        return -1;  // Return a sentinel value indicating underflow
    }
}

Code for the Peek Operation

The peek function returns the top element without removing it from the stack. If the stack is empty, it prints "Stack is Empty".

// Peek operation: Views the top element without removing it
int peek() {
    if (top != -1) {
        return stack[top];
    } else {
        cout << "Stack is Empty" << endl;
        return -1;  // Return a sentinel value indicating empty stack
    }
}

Code for the isEmpty Operation

The isEmpty function checks whether the stack is empty by verifying if top is -1.

// isEmpty operation: Checks if the stack is empty
bool isEmpty() {
    return top == -1;
}

Code for the isFull Operation

The isFull function checks whether the stack has reached its maximum size.

// isFull operation: Checks if the stack is full
bool isFull() {
    return top == MAX_SIZE - 1;
}

Full Code Implementation

Now, let's combine all the functions together and provide the complete implementation. We'll use a stack with a maximum size of 3 and demonstrate all operations.

//execute=true;
#include <iostream>
using namespace std;
 
#define MAX_SIZE 3  // Limiting the stack size to 3 for simplicity
 
class Stack {
private:
    int stack[MAX_SIZE];  // Array to store stack elements
    int top;              // Index of the top element
 
public:
    // Constructor to initialize the stack
    Stack() {
        top = -1;  // Initialize the top index to -1 (indicating the stack is empty)
    }
 
    // Push operation: Adds an element to the stack
    void push(int element) {
        if (top < MAX_SIZE - 1) {
            top++;
            stack[top] = element;
            cout << "Pushed " << element << " to stack." << endl;
        } else {
            cout << "Stack Overflow" << endl;
        }
    }
 
    // Pop operation: Removes the top element from the stack
    int pop() {
        if (top != -1) {
            int element = stack[top];
            top--;
            return element;
        } else {
            cout << "Stack Underflow" << endl;
            return -1;  // Return a sentinel value indicating underflow
        }
    }
 
    // Peek operation: Views the top element without removing it
    int peek() {
        if (top != -1) {
            return stack[top];
        } else {
            cout << "Stack is Empty" << endl;
            return -1;  // Return a sentinel value indicating empty stack
        }
    }
 
    // isEmpty operation: Checks if the stack is empty
    bool isEmpty() {
        return top == -1;
    }
 
    // isFull operation: Checks if the stack is full
    bool isFull() {
        return top == MAX_SIZE - 1;
    }
};
 
int main() {
    Stack s;
 
    s.pop();  // Attempting to pop when the stack is empty
 
    // Pushing elements onto the stack
    s.push(10);
    s.push(20);
    s.push(30);
 
    // Attempting to push when the stack is full
    s.push(40);  // This should trigger a stack overflow
 
    // Peeking the top element
    cout << "Top element is: " << s.peek() << endl;
 
    // Popping elements from the stack
    cout << "Popped element: " << s.pop() << endl;
    cout << "Popped element: " << s.pop() << endl;
 
    // Pushing more elements after popping
    s.push(40);
    s.push(50);
 
    // Final peek to show the current top element
    cout << "Top element is: " << s.peek() << endl;
 
    return 0;
}

Example Walkthrough and Explanation:

Attempt to Pop When Empty:
- s.pop() → Stack Underflow (since the stack is empty).
Push Operations:
- s.push(10) → Stack: [10]
- s.push(20) → Stack: [10, 20]
- s.push(30) → Stack: [10, 20, 30]
Attempt to Push When Full:
- s.push(40) → Stack Overflow (since the stack size is limited to 3).
Peek Operation:
- peek() → Returns the top element (30), and prints "Top element is: 30".
Pop Operations:
- pop() → Removes 30 (top element), now Stack: [10, 20].
- pop() → Removes 20 (next top element), now Stack: [10].
Push More Elements:
- s.push(40) → Stack: [10, 40]
- s.push(50) → Stack: [10, 40, 50]
Final Peek:
- peek() → Returns the top element (50), and prints "Top element is: 50".

Conclusion:

In this blog, we've explored the fundamentals of stacks, their key operations like push, pop, and peek, and how to implement a stack using arrays in C++. Understanding stacks is crucial as they are a fundamental data structure used in various algorithms and problem-solving tasks, such as function call management and expression evaluation. 📚

By mastering these basic concepts, you'll be well on your way to tackling more advanced topics in data structures and algorithms. Keep practicing, experimenting with different implementations, and stay curious—there’s always more to learn in the world of programming! 💡🚀

Happy coding! 🎉